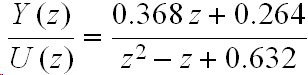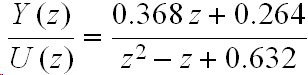Z-Transform Etudes

Discrete transforms are defined in the Z-domain which provides for convenient analysis of the transient response, stability, etc. of the system described by the transfer function. Given the transfer function and the forcing function, it is usually an easy task to compute the output from the system.

You can convert the transfer function into a time-domain difference equation by noting that, in the Z domain, each z^nY(z) term represents the output of the transfer function at the -n th sampling interval. z^0 Y(z) is the output of the transfer function at the current time. In the time domain, k represents the sampling time. y(k) is the output of the transfer function at the current time. y(k - 1) was the output at the previous sample time. If you solve the transfer function for Y(z), you can make a simple transfer to the time domain knowing the simple association that z^nY(z) is y(k + 1). The computation of the output of the transfer function is simply a sequence of multiplications and additions. Each coefficient is multiplied by a value of either the output or the input forcing function. If the computation of the current output is based entirely on past data, the value can be pre-computed. If the current input is an element of the calculation, you must wait to read the input to complete the calculation. If the caculation has any elements with k + n terms where n is positive, you have a problem.

For this Z-transform Etude, you are to write a QNX task that computes the response of this transfer function

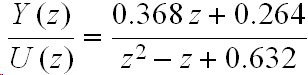
What to do

1. Determine the time-domain difference equation for the transfer function.
2. Write a QNX task that computes the transfer function's response to a step input of 5. Run the simulation for 1000 sampling intervals. Store the output values in a local array. When the task finishes computing the output values, open a file in /tmp and write the output values to that file. Give the file a .csv extension so that you can easily import the data into Excel to look at plots of the response to a step input. Use the Target File System Navigator view in Momentics to copy the file to the development workstation.
3. Next, run this calculation as a periodic task executing at a 10Hz period. During each execution, compute the output value and output it from the purplebox as an analog value through the channel 0 12-bit digital-to-analog converter (DAC). See the following notes for tips on working with the DAC.
4. Use a second task to control the simulation. This could be the default task that starts executing in main. This control task should accept input to allow the user to vary the input value, stop the simulation, write saved values to a file, and any other commands that you think might be useful. It may be useful to save both the output and input values when the simulation runs. When the application terminates, write them to the file in comma-separated-value format so that you can easily look at plots of the data using Excel.
5. You will probably not get to this point in this class, but if you do have time, a final step would be to provide the input value as an analog voltage that your program reads from one of the analog-to-digital converter input channels.

Notes

• If you do not finish all the steps above during this class time, use them as a guide for your work on the Real-Time Control project. The steps above outline the elements you need to develop to complete the project.
• The purplebox analog outputs are 12-bit digital-to-analog converters (DACs). If you configure the DAC to output a bipolar +/-10 volts, 0 outputs -10 volts (minus 10v); 2048 outputs 0 volts; 4095 outputs just under +10 volts.
• You will need to scale the output of the transfer function to the range of codes the DAC accepts.
  1. Determine the minimum and maximum output values that the transfer function generates for the input values that you want to use.
  2. You will do a linear scaling of transfer function output values (TFO) to DAC input codes (DIC). One point on the linear scale will be (TFO, DIC) = (0, 2048). The second point will be the positive or negative TFO which has the largest absolute value mapped to 4095 or 0, respectively. You may want to map a slightly more positive or more negative TFO value to the end of the DIC range for a safe zone to make sure that you do not saturate the output of the DAC.
  3. To compute the DAC code, compute the linear transform defined by the two points found in step 2. The input to the transform is the TFO. The output of the transform is the value that you output to the DAC.
• There is information about working with the DACs in the Athena manual. Pages 57 through 60 have information about using the analog outputs. The data acquisition system I/O map and register descriptions start on page 36.
• Be very careful when working with the DICs. Their input is a 12 bit value split across two I/O registers. These should be defined as unsigned values. Be very careful when manipulating these values. Unintentional sign extension can cause you a number of problems.
• There is a webpage on accessing device registers in the Working with QNX section of the Lab Information webpage page.
• The Data Translation DT9812 data acquisition device provides a set of instruments under the Quick DataAcq application. You can measure the voltage the DAC is outputting, show an oscilloscope trace, and, probably the most useful, do a strip chart recording that can be written to a file.
• Here is an Excel workbook that calculates this transfer function's response to a step input of 5. You can compare your answer to the values shown in that workbook.
• Any files that you write in /tmp will be erased on the next purplebox reset.

Submission Instructions

• At the end of class, submit your QNX source and include files for as far as you got with the assignment to the Z-transform Etudes dropbox in myCourses. Be sure to include your name and your teammate's name in the description when you deposit your files.